동적 배열
- 크기가 고정되어 있어 할당한 크기보다 많은 갯수의 데이터를 저장할 수 없는 배열과는 달리 유동적으로 저장공간을 resize할 수 있는 자료구조이다.
- 정적 배열과 동적 배열의 차이점은 초기화 시 크기를 지정할 필요가 없다는 것이다.
- 다양한 언어에서 동적 배열에는 기본 크기가 할당될 수 있다.(예를 들어 Java는 10이고, C#은 4이다.)그러나 이들은 운영 체제에 의해 동적으로 크기가 조정된다.
- 동적(Dynamic) 프로그래밍 언어 중 하나인 파이썬은 대부분의 동적 언어들이 그렇듯 정적 배열을 지원하지 않고, '리스트(list)' 자료형만을 동적 배열로써 제공한다.
동적 배열의 동작원리
배열이 동적인 경우, 용량이 부족할 때 다른 요소를 추가하는 것은 원래 크기의 두 배인 새로운 배열로 값들을 복사하여 이루어진다.모든 요소가 복사된 경우, 기존것을 계속 메모리에 유지하는 것은 의미가 없기에 메모리에서 해제된다(deallocate).
이 작업은 분할 상환된 시간 복잡도인 amortized O(1)에 따라 실행된다. 분할 상환 시간 복잡도는 각 연산당 평균적으로 소요되는 시간으로, 한 번 발생하면 장기간 동안 다시 발생하지 않아 비용이 "분할 상환"되게 됨을 의미한다. 이는 배열이 항상 크기를 조정해야 하는 것이 아니기 때문에 합리적이다.
왜 용량을 두 배로 늘릴까?
용량이 부족할 때 초기 배열 크기를 두 배로 늘리는 이유에 대해 알아보자.
아래의 시각적 표현은 크기가 8인 결과 배열을 보여준다. 이제 동적으로 채워 넣고자 하며 크기가 1인 배열로 시작한다고 상상해보십시오. 5를 추가하고, 공간을 두 배로 늘려 6을 추가하고, 그 공간을 다시 두 배로 늘려 7과 8을 추가하고, 그 공간을 다시 두 배로 늘려 9, 10, 11 및 12를 추가한다.

위 배열의 크기는 1 -> 2 -> 4 -> 8로 변경되었다. 여기서 패턴은 마지막 항(지배 항)이 항상 그 앞의 모든 항의 합보다 작거나 같다는 것이다. 이 경우, 1 + 2 + 4 = 7이고, 7 < 8이다. 크기가 8인 결과 배열을 생성하기위해서는, 7에 8을 더하면 총 15개의 작업이 필요하다. 일반적으로 공식은 임의의 배열 크기 n에 대해 최대 O(2n)의 작업이 소요되며, 이것은 O(n)이라 할 수 있다.
왜 append()의 시간 복잡도가 O(1)로 간주될까?
(+ 새 배열의 크기를 기존 배열의 크기의 2배로 늘리는 이유는?)
배열이 꽉 찼을 때 append()를 호출하면 resize()를 해야하므로 해당 순간의 시간 복잡도는 O(N)이 된다.
그러나 평균적으로 한 번씩 resize()를 하더라도 append()의 시간 복잡도는 O(1)이 된다.
새 배열의 크기를 기존 배열의 크기의 2배로 늘리면 append()의 평균 수행 시간이 O(1)이 되기 때문에 선택된다.
새 배열의 크기를 기존 배열의 크기의 2배로 늘리면, 데이터를 복사할 때마다 복사되는 데이터의 수가 1개, 2개, 4개, 8개 ... 등의 등비수열을 이룬다. 이렇게 함으로써 resize() 시 복사되는 데이터의 수가 일정한 규칙을 가지게 되어, 평균적으로 append()의 시간 복잡도를 O(1)로 유지할 수 있다.
즉, 새 배열의 크기를 기존 배열의 크기 보다 2배씩 늘려야 append()의 평균 수행시간이 O(1) 이 된다.
예를들어 배열을 재할당할 때 크기를 상수만큼 늘린다고 가정해보자.
K = resize() 호출 수 (재할당 횟수)
M = 재할당하는 배열의 크기 단위
N = append() 호출 수 ( 저장할 총 데이터 개수)
처음에 빈 배열을 만들어서 데이터를 N개 만큼 추가 한다( append()를 N번 호출한다. )
기존 배열의 공간이 가득차면 resize() 를 호출해야하고 새 배열의 크기는 기존배열 보다 M 만큼 늘어나기 때문에
resize() 호출수(K) 는 다음과 같다.
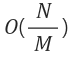
즉, 데이터를 1,000(N) 개를 넣을 때 배열의 재할당 크기를 10(M) 이라고 하면 재할당(K)은 100번 일어난다. (데이터를 10개 넣고나면 배열이 가득 차서 배열의 크기를 계속 새로 늘려주기때문에)
여기서 M 은 상수 이기 때문에 N 이 커질수록 M 값이 미치는 영향은 작아진다.따라서 resize() 의 시간복잡도(K)는 O(N) 이 된다. ( M이 10이든 100이든 상수는 결국 시간복잡도에 영향을 주지 못한다. )
배열을 재할당 할 때 마다 새 배열에 복사되는 데이터의 수는 각 M개, 2M개,3M...KM개 이다. (위 예시로 따지면 10개,2*10개,3*10개...100*10개 순으로 배열 증가)
N개의 데이터를 넣으면서 복사되는 데이터의 수를 모두 더하면 (1+2+3++K)M 이므로 정리하면 복잡도는 다음과 같다.
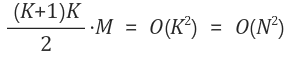
위를 N 으로 나누어서 평균을 내면 O(N) 이 되어 append() 평균 수행시간은 O(N) 이 되버린다.
하지만 배열의 크기를 기존 배열 크기의 2배씩 늘리게 되면 배열을 재할당 할 때 마다 새 배열에 복사되는 데이터의 수는 각 1개, 2개, 4개, 8개,...2^(k-1) 개 이다.
N개의 데이터를 넣으면서 복사되는 데이터의 수를 모두 더하면 1+2+4+8+...+2^(k-1)이므로, 등비수열의 합 공식 에 따라 2^k-1이 된다. 여기서 배열의 크기가 2배씩 증가하기 때문에 마지막인 1 번째 부터 K-2 번째 까지의 합이 K-1 번째 값과 거의 같다. K-1 번째 resize() 의 시간복잡도는 O(N) 일 것이기 때문에 결국은 1 번째 부터 K-1 번째 까지 데이터를 복사한 수행시간은 기껏 해야 O(2N) 일 것이고 결국 append()의 총 수행시간은 O(N) 이 된다. 따라서 배열의 크기가 2배씩 증가할 때 append()의 평균수행 시간은 O(N)을 N으로 나눈 O(1)이라고 할 수 있다.
분할 상환 분석(Amortized Analysis)
분할 상환 분석(Amortized Analysis)은 Big-O(빅오)와 마찬가지로, 함수의 동작을 설명할 때 중요한 분석 방법 중 하나이다.
동적 배열은 분할 상환 분석의 대표적인 예이다.
동적 배열은 미리 초깃값을 작게 잡아 배열을 생성한 후, 데이터가 추가되어 배열이 꽉 찰 때마다, 배열의 크기를 늘려주고 값을 모두 복사하는 방식으로 구현된다. 배열의 크기를 늘려나가는 배율을 '그로스 팩터(Growth Factor, 성장 인자)'라고 일컫는다. 대개는 더블링(Doubling)이라 하여 그로스 팩터를 2로 한다. (각 언어마다 늘려가는 비율은 상이하다.)
Big-O vs Amortized Analysis
- 동적 배열에서 데이터를 추가하는 작업의 비용은 O(1)이다.
- 더블링이 일어났을 때의 비용, 즉 배열의 크기를 늘려주고 값을 모두 복사하는 작업의 비용은 O(N)이다.
그렇다면 동적 배열에서 삽입의 시간 복잡도는 O(N)일까 O(1)일까? 더블링이 발생하는 경우는 어쩌다 한 번뿐임에도 불구하고 그렇다고 표현하는 것은 지나치게 비관적이고 정확하지도 않다. 이러한 때에 분할 상환 분석을 이용한다.
이는 최악의 경우를 여러 번에 걸쳐 골고루 나눠주는 형태로 시간 복잡도를 계산하는 분석 방식이다. 이를 통해 동적 배열에서 일어나는 삽입의 시간 복잡도를 Amortized O(1)이라고 표현할 수 있다.
관련문제 (Concatenation of Array)
https://leetcode.com/problems/concatenation-of-array/
LeetCode - The World's Leading Online Programming Learning Platform
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com
Python
class Solution:
def getConcatenation(self, nums: List[int]) -> List[int]:
ans = []
for i in range(2):
for n in nums:
ans.append(n)
return ansJava
class Solution {
public int[] getConcatenation(int[] nums) {
int[] ans = new int[nums.length*2];
for(int i=0; i<nums.length; i++){
ans[i] = nums[i];
ans[i+nums.length] = nums[i];
}
return ans;
}
}'자료구조&알고리즘' 카테고리의 다른 글
| [자료구조&알고리즘] 유클리드 호제법 최대/최소공배수 구하기 (PYTHON, JAVA) (0) | 2024.04.01 |
|---|---|
| [자료구조 / 알고리즘] Heap / PriorityQueue (0) | 2024.03.19 |
| [자료구조] 스택 Stack (Python,Java) (0) | 2023.10.12 |
| [자료구조] 스택 Stack (JAVA, PYTHON) (0) | 2023.09.23 |
| [자료구조] 정적 배열 Static Arrays (0) | 2023.09.18 |
