
✔ 문제 019 K번째 수 구하기
⬜ 핵심 아이디어
퀵 정렬(quick sort)은 기준값(pivot)을 선정해 해당 값보다 작은 데이터와 큰 데이터로 분류하는 것을 반복해 정렬하는 알고리즘이다. 기준값이 어떻게 선정되는지가 시간 복잡도에 맣은 영향을 미치고, 평균적인 시간 복잡도는 O(nlogn)이다.pivot을 중심으로 계속 데이터를 2개의 집합으로 나누면서 정렬하는 것이 퀵 정렬 핵심이다.
특히, 문제에서는 값의 위치를 한번 정하면 그 후 변하지 않기에 다 정렬하지 않고 그 값을 구한다.
+) 데이터가 대부분 정렬되어 있는 경우 앞쪽에 있는 수를 pivot으로 선택하면 불필요한 연산이 많아진다.앞쪽에 있는 수를 피벗으로 선택하면, 피벗을 기준으로 배열이 두 부분으로 나뉘는데,이때 정렬된 배열에서는 피벗을 기준으로 한 부분이 상당히 큰 부분이 되기 때문이다.
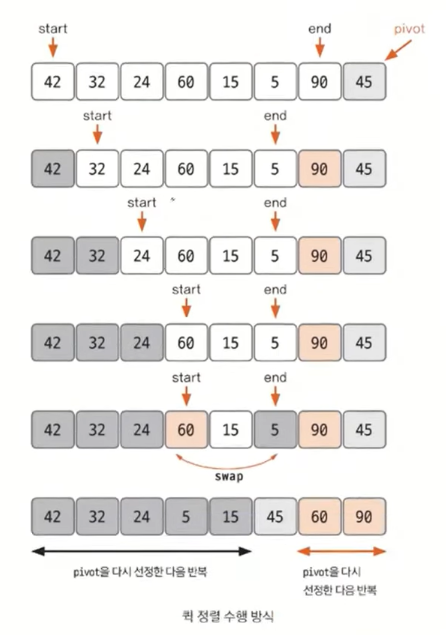
⬜ 삽입 정렬 수행 방식
-
- 데이터를 분할하는 pivot을 설정한다(위 그림의 경우 가장 오른쪽 끝을 pivot으로 설정).
- pivot을 기준으로 다음 a~e 과정을 거쳐 데이터를 2개의 집합으로 분리한다.
- 2-a. start가 가리키는 데이터가 pivot이 가리키는 데이터보다 작으면 start를 오른쪽으로 1칸 이동한다.
2-b. end가 가리키는 데이터가 pivot이 가리키는 데이터보다 크면 end를 왼쪽으로 1칸 이동한다.
2-c. start가 가리키는 데이터가 pivot이 가리키는 데이터보다 크고, end가 가리키는 데이터가 pivot이 가리키는 데이터보다 작으면 start, end가 가리키는 데이터를 swap하고 start는 오른쪽, end는 왼쪽으로 1칸씩 이동한다.
2-d. start와 end가 만날 때까지 2.a ~ 2.c를 반복한다.
2-e. start와 end가 만나면 만난 지점에서 가리키는 데이터와 pivot이 가리키는 데이터를 비교하여 pivot이 가리키는 데이터가 크면 만난 지점의 오른쪽에, 작으면 만난 지점의 왼쪽에 pivot이 가리키는 데이터를 삽입한다. - 분리 집합에서 각각 다시 pivot을 선정한다.
- 분리 집합이 1개 이하가 될 때까지 과정 1~3을 반복한다.
슈도코드 작성하기
N(숫자 개수) K(K번째 수)
A(숫자 데이터 저장 배열)
for(N만큼 반복){
A 배열 저장하기
}
퀵 소트 실행하기
K번째 데이터 출력하기
[별도의 함수 구현 부분]
퀵 소트 함수(시작, 종료, K)
{
피벗 구하기 함수(시작, 종료)
if(피벗==K) 종료
else if(K < 피벗) 퀵 소트 수행하기(시작, 피벗-1, K)
else 퀵 소트 수행하기(피벗 + 1, 종료, K)
}
피벗 구하기 함수(시작, 종료)
{
데이터가 2개인 경우는 바로 비교하여 정렬
M(중앙값)
중앙값을 시작 위치와 swap
pivot(피벗)을 시작 위치 값 A[S]로 저장
i(시작점), j(종료점)
while(i<=j)
{
피벗보다 큰 수가 나올 때까지 i++
피벗보다 작은 수가 나올 때까지 j--
찾은 i와 j 데이터를 swap
}
피벗 데이터를 나눠진 두 그룹의 경계 index에 저장하기
경계 index 리턴
}JAVA
import java.util.*;
import java.lang.*;
import java.io.*;
// Please name your class Main
class Main {
public static void main (String[] args) throws java.lang.Exception {
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(in.readLine());
int N = Integer.parseInt(st.nextToken());
int K = Integer.parseInt(st.nextToken());
st = new StringTokenizer(in.readLine());
int[] A = new int[N];
for(int i = 0; i < N; i++){
A[i] = Integer.parseInt(st.nextToken());
}
quickSort(A, 0, N - 1, K - 1); //배열, 시작점, 끝점, K번째(index)
System.out.println(A[K - 1]);
}
public static void quickSort(int[] A, int S, int E, int K){
if(S < E){
int pivot = partition(A, S, E);
if(pivot == K){ // K번째 수가 pivot이면 더이상 구할 필요 없음
return;
}
else if(K < pivot){ // K가 pivot보다 작으면 왼쪽 그룹만 정렬 수행하기
quickSort(A,S,pivot-1, K);
}
else{ // K가 pivot보다 크면 오른쪽 그룹만 정렬 수행하기
quickSort(A,pivot+1,E,K);
}
}
}
public static int partition(int[] A, int S, int E){
if(S + 1 == E){ // data 두개인 경우는 바로 비교하여 정렬
if(A[S] > A[E]) swap(A, S, E);
return E;
}
int M = (S + E) / 2;
swap(A, S, M); // 배열에서 중앙값을 1번째 요소로 이동하기(가독성위함)
int pivot = A[S];
int i = S + 1, j = E; // 투 포인터 설정
while(i <= j){
while(j >= S + 1 && pivot < A[j]){ //pivot보다 작은 수가 나올 때까지 j-- (크면 왼쪽으로 계속이동)
j--;
}
while(i <= E && pivot > A[i]){ //pivot보다 큰 수가 나올때까지 i++ (작으면 오른쪽으로 계속이동)
i++;
}
if(i <= j){ // 찾은 i와 j 데이터를 swap
swap(A,i++,j--);
}
}
// 피벗 데이터를 나눠진 두 그룹의 경계 index에 저장하기
A[S] = A[j];
A[j] = pivot;
return j; // 경계 인덱스 리턴
}
public static void swap(int[] A, int i,int j){
int temp = A[i];
A[i] = A[j];
A[j] = temp;
}
}PYTHON
method 1. ipos
- 한 방향으로만 탐색하면서 정렬하는 방법이다.
- ipos에서 i는 배열을 쭉 돌며 pivot 값과 value를 비교한다.
- pos는 pivot 자리를 정하는 역할을 한다.
- pivot보다 작은 arr[i]이 있다면 arr[pos]값과 swap 후 pos+=1을 한다.
퀵 정렬은 기본적으로 O(nlogn)의 시간복잡도를 가지지만, ipos 방법은 0부터 돌기 대문에 이 경우 최악의 시간 복잡도인 O(n^2)를 가질 수 있다.이 때문에 모든 케이스를 테스트하는 백준에서는 시간초과가 쓴다.
import sys
input = sys.stdin.readline
def Qsort(lt, rt):
if lt < rt:
pos = lt
pivot = arr[rt]
for i in range(lt, rt):
if arr[i] <= pivot:
arr[i], arr[pos] = arr[pos], arr[i]
pos += 1
arr[rt], arr[pos] = arr[pos], arr[rt]
if pos == k-1:
print(k)
sys.exit(0)
Qsort(lt, pos-1)
Qsort(pos+1, rt)
if __name__ == "__main__":
n, k = map(int, input().split())
arr = list(map(int, input().split()))
Qsort(0, n-1)
method 2. 정석적인 퀵 정렬 방법 (양방향 탐색)
import sys
input = sys.stdin.readline
n, k = map(int, input().split())
a = list(map(int, input().split()))
def quickSort(s, e, k):
global a
if s < e:
pivot = partition(s, e)
if pivot == k:
return
elif k < pivot:
quickSort(s, pivot-1, k)
else:
quickSort(pivot+1, e, k)
def swap(i,j):
global a
tmp = a[i]
a[i] = a[j]
a[j] = tmp
def partition(s, e):
global a
if s + 1 == e:
if a[s] > a[e]:
swap(s, e)
return e # pivot return (정렬 후 첫번째 수)
m = (s+e) // 2 # 중앙값 구하기
swap(s, m) # pivot 맨 앞으로
pivot = a[s]
i = s+1
j = e
while i <= j:
while pivot < a[j] and j >= (s+1): # 피벗보다 작은 수가 나올 때까지 j--(피벗보다 크면 계속 왼쪽으로)
j = j-1
while pivot > a[i] and i <= e: # 피벗보다 큰 수가 나올 때까지 i++(피벗보다 작으면 계속 오른쪽으로)
i = i+1
if i <= j:
swap(i,j)
i = i+1
j = j-1
a[s] = a[j] # 최종적으로 i,j만난 인덱스경계를 pivot과 교환(바꾸기)
a[j] = pivot
return j
quickSort(0, n-1, k-1) # k-1배열에서 찾는수 ( k번째->인덱스로는 k-1번째 인덱스 )
print(a[k-1])
개념을 아는것과 직접 구현해보는것은 천지차이인것같다.

'자료구조&알고리즘 > 알고리즘_코딩테스트' 카테고리의 다른 글
| [알고리즘_코딩 테스트_JAVA] 그래프-유니온 파인드 (JAVA, PYTHON) (0) | 2024.03.19 |
|---|---|
| [알고리즘_코딩 테스트_JAVA] 그래프-이분 그래프 판별하기 (JAVA, PYTHON) (0) | 2024.03.19 |
| [알고리즘_코딩 테스트_JAVA] 삽입 정렬-ATM (JAVA, PYTHON) (0) | 2024.01.19 |
| [알고리즘_코딩 테스트_JAVA] 선택 정렬 (JAVA, PYTHON) (1) | 2024.01.04 |
| [알고리즘_코딩 테스트_JAVA] 버블 소트 프로그램 1 (JAVA, PYTHON) (0) | 2024.01.01 |
