✅ BST (Binary Search Tree, 이진 탐색 트리)
- 자식 노드 수: 최대 2개
- 정렬 규칙: 왼쪽 자식 < 부모 < 오른쪽 자식
- 시간 복잡도: 평균 O(log N), 최악의 경우 O(N) (비균형 시)
- 단점: 노드 수가 많을수록 트리의 높이가 커져 비효율 발생 가능
✅ B-Tree (Balanced Tree)
BST를 확장한 구조로, 대용량 데이터 처리에 적합한 균형 잡힌 트리
- 한 노드에 여러 개의 키와 자식 노드를 가짐
- 자식 노드 수: 3개 이상 가능 (차수 M 이상)
- 키 저장: 오름차순 정렬
- Balanced Tree: 삽입/삭제 후에도 항상 균형 유지
- 모든 리프 노드가 같은 깊이에 존재
🤘🏻 B-Tree 규칙
| 자식 수 (최대) | M개 (M = 차수) |
| 키 수 (최대) | M - 1개 |
| 최소 자식 수 | ⌈M / 2⌉개※ 루트/리프 제외 |
| 최소 키 수 | ⌈M / 2⌉ - 1개※ 루트/리프 제외 |
내부 노드 규칙은 다음과 같다.
- 내부 노드에 키 수가 x개이면 자식 노드는 x + 1개
- 내부 노드는 최소한 2개의 자식 노드를 가짐
- → 이는 어떤 차수(M)이든 성립
🔷B-tree 삽입 동작 원리, 시뮬레이션
리프노드가 가득차지 않았다면, 오름차순으로 k를 삽입한다.
리프노드가 가득찼다면 일단 삽입 후, 그래서 중간값을 기준으로 노드를 나눈다 (→ 노드 분할).
중앙값은 부모 노드로 올라가고, 작은 값들은 왼쪽 자식, 큰 값들은 오른쪽 자식이 된다.
삽입 규칙을 요약하면 아래와 같다.
🛠 B-tree 삽입 규칙 요약
- 항상 리프 노드에 삽입
- 정렬 유지 (키는 오름차순 정렬)
- 노드가 넘칠 경우
- 가운데 키(Median) → 부모 노드로 승진
- 좌우로 분할(split)
- 부모도 넘치면 재귀적으로 분할 & 승진, 루트도 포함
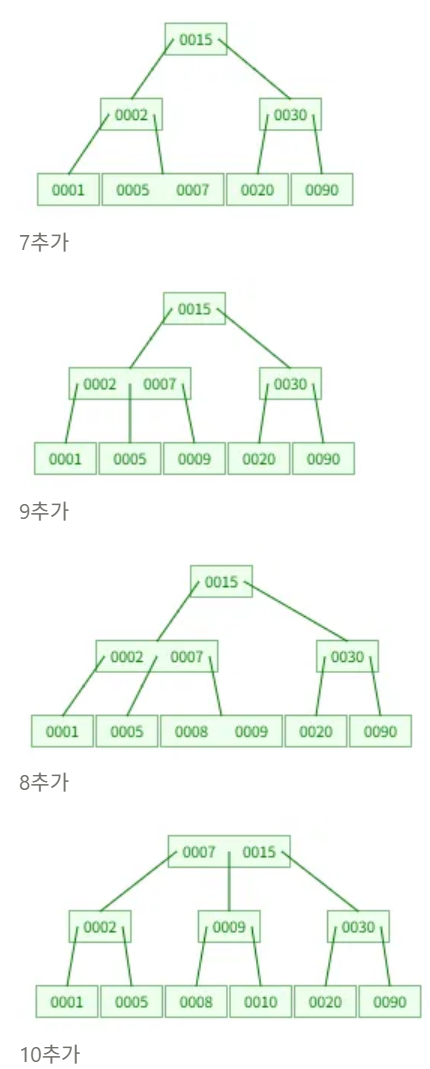
이해를 돕기 위해 간단한 삽입 시뮬레이션을 해보자.
| 1 → 15 → 2 → 5 → 30 → 90 → 20 → 7 → 9 → 8 → 10 → 50 → 70 → 60 → 40 순으로 삽입 |


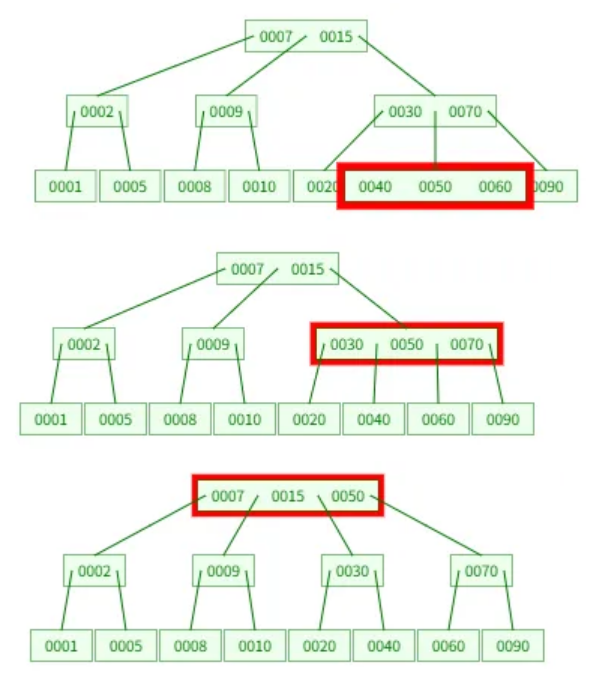
마지막 40이 추가되는 과정을 자세히 나타내 봤다. 리프에 추가후, 중앙값(50)을 위로 올리고 분할(40,60)한다.
다시 노드가 넘치므로 루트까지 분할과정을 수행한다.
🔷B-tree 삭제 동작 원리, 시뮬레이션
- 삭제는 항상 리프 노드에서 실행된다.
- 내부 노드 삭제 시 → 선행자 또는 후행자 키와 교환 후, 리프에서 삭제
- 삭제 후 underflow(키 개수 부족) 발생 시 재조정 필요
- 조건: 노드의 키 수 < 최소 키 수 (보통 ⌈M/2⌉ - 1)
- 재조정 방법: 총 3가지
- 형제 노드에게 키 빌리기 (Redistribution)
- 형제와 병합 (Merge)
- 루트 축소 (트리 높이 감소)
🛠 B-tree 삭제 규칙 요약
① 리프 노드에서 삭제
- 삭제 후 최소 키 수 이상 유지되면 → 아무 문제 없음
② Underflow 발생 시 재조정
②-1. 형제에게서 키 빌리기 (Redistribution)
- 형제 노드가 여유 키(최소 초과)를 가진 경우
- 형제의 키 하나를 부모로 올리고
- 부모의 키 하나를 내려와서 underflow 노드에 채움
②-2. 병합 (Merge)
- 형제도 최소 키 수만 갖고 있어 빌릴 수 없을 때
- 형제 + 부모의 키 1개 + underflow 노드를 합쳐 하나의 노드로
- 부모 노드는 키와 자식 포인터 1개를 잃고 → 부모도 underflow 가능 → 재귀적 처리
②-3. 루트 축소
- 루트 노드의 키가 모두 없어지면
- 루트 삭제
- 자식 노드가 새로운 루트가 되며 트리 높이 감소
CF) 내부 노드의 키 삭제 시:
- 선행자(왼쪽 서브트리의 최댓값) 또는 후행자(오른쪽 서브트리의 최솟값) 과 교체
- 교체한 키는 리프 노드에 있으므로 → 리프에서 삭제 실행
- 이후 리프 삭제 로직대로 처리 (underflow 포함)
※ 이렇게 하면 "삭제는 항상 리프 노드에서"라는 원칙이 유지됨
이해를 돕기 위해 삭제 케이스 예제들을 살펴보자.
예시 1: 리프에서 삭제만


예시 2: 내부 노드 삭제 → 리프 선임,후임자와 swap 후 삭제

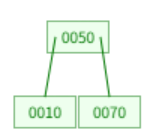
예시 3: 키 삭제 후 underflow → 형제에게 키 빌림

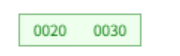
10 삭제 → [ ] underflow, 형제 [30]도 최소 키 수 → 부모로부터 키내려받고 형제노드 20과 병합 → [20, 30] → 루트 제거, 트리 높이 1 감소
왜 DB Index에 B Tree 자료구조를 쓰는가?
데이터베이스는 보통 SSD나 HDD 같은 세컨더리 스토리지(보조 기억장치)에 저장된다.
이런 저장소는 RAM보다 훨씬 느리지만 대신 용량이 크고 전원이 꺼져도 데이터가 남아있다.
핵심: 세컨더리 스토리지는 느리니까, 여기 접근을 최소화하는 것이 성능의 핵심이다!!!
AVL 트리 vs B-tree
AVL 트리
- 노드당 자식: 2개
- 노드당 데이터: 1개
- 탐색 시: 리프 노드까지 여러 번 내려가야 함 → 세컨더리 스토리지 접근이 많아짐
B-tree (예: 5차 B-tree)
- 노드당 자식: 최대 5개
- 노드당 데이터: 최대 4개
- 탐색 시: 더 넓은 범위로 한 번에 검색, 깊이가 얕음 → 접근 횟수 적음
예시: 같은 데이터를 찾을 때
- AVL 인덱스는 4번 블록 접근
- B-tree 인덱스는 2번 블록 접근
→ 차이가 작아 보여도 DB에서는 엄청 큰 성능 차이를 불러온다!
B-tree는 블록📦을 잘 활용한다. 세컨더리 스토리지는 "블록 단위"로 데이터를 읽는다.세컨더리 스토리지는 데이터를 4KB 같은 '블록 단위'로 읽는다. 그런데 AVL 트리는 노드 1개에 데이터 1개밖에 없어서, 블록의 대부분이 빈 공간으로 낭비된다. 반면 B-tree는 한 노드에 여러 개의 데이터를 저장해 블록 하나에 쓸모 있는 데이터가 가득 들어간다!
즉, 한 번 블록을 읽을 때 가능한 많은 유효 데이터를 담아야 성능이 좋다.
- AVL 트리: 한 블록에 1개 데이터만 있을 수 있음
- B-tree: 한 블록에 4~100개 데이터까지 있을 수 있음
👉 같은 블록을 읽더라도 B-tree는 훨씬 더 많은 유의미한 데이터를 담을 수 있어서 효율적이다.
B-tree의 강력함을 숫자로 본다면 더욱 강력하다🔥
101차 B-tree를 예로 들어보자. (각 노드가 최대 100개의 데이터, 101개의 자식을 가짐)
| 3 | 1억 개 이상! 😲 |
| 4 | 수십억 개도 가능 |
즉, 단 3~4단계 탐색만으로 수천만 개 데이터를 빠르게 조회할 수 있다는 뜻이다.
❓ 그럼 AVL이나 해시 인덱스는 언제 쓸까?
- AVL: 메모리 기반 데이터나 캐시처럼 I/O 걱정 없는 상황에 적합
- 해시 인덱스: 동등 비교(=)에만 빠르고 좋음.
하지만 범위 조회(<, >)나 정렬엔 못 쓴다!
대부분의 SQL 쿼리는 범위 검색도 하니까 → B-tree 계열이 훨씬 적합!
✅ B+Tree (Balanced Plus Tree)
- 모든 데이터는 리프 노드에만 저장
- 내부 노드는 key만 저장 (데이터 없음)
- 리프 노드끼리는 오른쪽으로 연결 리스트처럼 연결되어 있음
🔷B+tree 삽입 동작 원리
B+트리 삽입
노드가 가득 찼을 때(split 발생)
→ 중간 key는 부모로 올리고,
→ 오른쪽 리프 노드에는 중간 key도 포함시켜 유지
→ 리프 노드는 왼쪽 → 오른쪽으로 연결리스트 형태로 유지
B트리는 중간 key를 부모에만 올리지만, B+트리는 리프에도 그대로 남긴다는 점이 중요!
B+트리 삭제 요약 (B트리와의 차이)
삭제 후 key 수가 부족하면 → 병합 또는 재분배가 필요.
B+트리는 리프 노드 간에만 병합/재분배
→ 병합 시 부모 key는 끌어오지 않음!
→ 형제 리프끼리만 병합하고 부모 key는 자동 제거 or 업데이트
왜 B+ Tree가 더 효율적일까?
B+ Tree는 범위 검색에 강하고, 트리 구조가 평평해 검색 속도가 빠르다.
1️⃣ 범위 검색에 강하다
- 리프 노드끼리 연결 리스트로 이어져 있어서,
한 번 찾은 후 → 옆으로 쭉 탐색 가능! - 예: WHERE score BETWEEN 80 AND 90
→ 80 찾은 뒤 → 오른쪽 리프만 순차적으로 따라가면 끝!
👉 연속된 데이터 조회에 최적화된 구조
2️⃣ 트리의 높이가 낮고, 더 균형 잡힘
- 내부 노드는 key만 저장하고 value는 리프에만 저장
→ 한 노드에 더 많은 key를 넣을 수 있음
→ 분할이 덜 발생하고
→ 트리의 높이가 낮아짐
✔️ 트리가 낮다는 건 = 검색할 때 디스크 접근 횟수(I/O)가 적다는 뜻!
👉 검색 속도도 더 빠름
B트리 vs B+트리
| 내부 노드에 저장되는 것 | key + value | key만 저장 |
| 리프 노드 | key + value | key + value (모든 value는 여기만) |
| 한 노드에 들어갈 수 있는 key 수 | 적음 (value도 같이 저장하니 공간 제한) | 많음 (key만 저장하니 공간 여유) |
| 결과 | 자주 분할됨 → 트리 높이 ↑ | 덜 분할됨 → 트리 높이 ↓ |
| 검색 시 디스크 접근 | 더 많을 수 있음 | 더 적음 (얕은 구조) |
'자료구조&알고리즘' 카테고리의 다른 글
| 2025 답/해설 없는 최신 코테 풀이 도전 메모기록 - 3 (2) | 2025.05.14 |
|---|---|
| 2025 답/해설 없는 최신 코테 풀이 도전 메모기록 - 2 (1) | 2025.05.01 |
| [programmers] 붕대 감기 (Python 풀이) (0) | 2025.04.23 |
| 2025 답/해설 없는 최신 코테 풀이 도전 메모기록 (0) | 2025.02.08 |
| [일간코테] 주사위 고르기 (Python, Java) (2) | 2024.11.15 |
